此博客停更

//求轻喷 ↗大神右上角

因为网络流的模型实在是太经典了，于是在这里就不再多废口舌讲模型，看下面这题吧

poj1273 Drainage Ditches

Dinic算法核心就是：

①在残量网络上跑层次图

②用dfs在层次图上增广，直到不存在增广路

③重复上述步骤直到不能再增广

用一张图来表示Dinic的流程就是这样的：

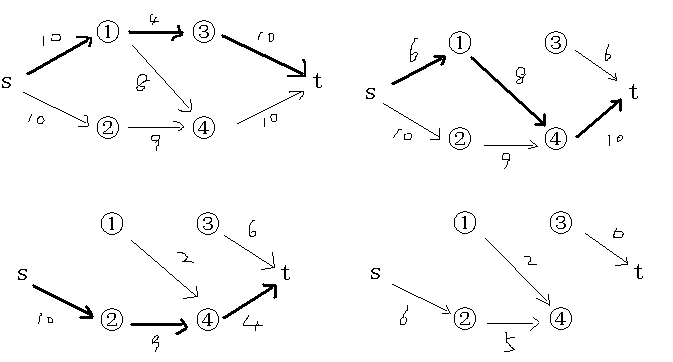
Dinic的思想概念是很好理解的，它的总时间复杂度为O(n²m)，实际上Dinic跑的比这个理论上的时间复杂度要快的多。

下面给出上面那题的AC代码做模板用：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define oo (1<<30)
#define N 100005
#define M 1000005
int n,S,T,ll,son[N],d[N],q[N],link[M],next[M],cap[M],opp[M];
#define min(a,b) (a<b?a:b)
bool bfs(){
	int x,y,l=1,r=1;
	memset(d,-1,sizeof(int)*(n+5));
	q[1]=S;d[S]=0;
	while(l<=r){
		x=q[l++];
		for(int i=son[x];i!=-1;i=next[i]){
			y=link[i];
			if(cap[i]&&d[y]==-1){
				d[y]=d[x]+1;q[++r]=y;
				if(y==T)return 1;
			}
		}
	}
	return 0;
}
int find(int now,int flow){
	int ret,y,w=0;
	if(now==T)return flow;
	for(int i=son[now];i!=-1&&w<flow;i=next[i]){
		y=link[i];
		if(cap[i]&&d[y]==d[now]+1&&(ret=find(y,min(flow-w,cap[i]))))
			cap[i]-=ret,cap[opp[i]]+=ret,w+=ret;
	}
	if(!w)d[now]=-1;
	return w;
}
void addedge(int x,int y,int z){
	link[++ll]=y;next[ll]=son[x];son[x]=ll;cap[ll]=z;opp[ll]=ll+1;
	link[++ll]=x;next[ll]=son[y];son[y]=ll;cap[ll]=0;opp[ll]=ll-1;
}
int main(){
	int m,x,y,z,ans,flow;
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	while(~scanf("%d%d",&m,&n)){
		memset(son,-1,sizeof(int)*(n+5));
		S=1;T=n;ans=0;ll=0;
		for(int i=1;i<=m;++i)
			scanf("%d%d%d",&x,&y,&z),addedge(x,y,z);
		while(bfs())
			while(1){
				flow=find(S,oo);
				if(!flow)break;
				ans+=flow;
			}
		printf("%d\n",ans);
	}
}

其实网络流注重的并非是怎么算网络流，用什么算法，关键是建模

习题：

poj3281Dining

poj2455Secret Milking Machine

loading...