Orz 叶队
矩阵乘法,即矩阵相乘→_→,公式:C[i][j] = Sigma(A[i][k] * B[k][j])
写成代码形式就是这样↓
for(int i=1;i<=n;i++) for(int j=1;j<=p;j++) for(int k=1;k<=m;k++) c[i][j]+=a[i][k]*b[k][j];
……嘛,很简单的啦,给道题先→_→
http://codevs.cn/problem/1287/
既然会了矩阵乘法。。那么矩阵乘法有什么用呢(赶脚一点都不实用啊)
——它可以用来优化DP
例题→求Fibonacci数列第N项。
先想到递推公式 F(n)=F(n-1)+F(n-2)
虽然这样递推已经很快了,但是矩阵乘法可以做的更快
思考如何从 (n-1,n)转移到(n,n+1)————乘上一个矩阵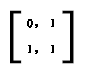 即可
即可
于是可以发现,乘上一次这个矩阵就是转移一次,乘上两次便是转移两次,所以只要乘上此矩阵的某某次方 便能得到答案~
于是回忆快速幂是怎么样的。。似乎是这样的↓
int quickpow(int m,int n,int k){
int b=1;
while(n>0){
if(n&1)b=(b*m)%k;
n=n>>1;
m=(m*m)%k;
}
return b;
}
想象一下b,m是矩阵类型,这也是灰常简单的→_→,代码大概是这样的↓↓
struct node{
long long k[3][3];
}m,tt;
node ju(node a,node b){
node c;
memset(c.k,0,sizeof(c.k));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++){
c.k[i][j]=0;
for(int k=1;k<=2;k++){
c.k[i][j]+=(a.k[i][k]*b.k[k][j])%p;
c.k[i][j]=c.k[i][j]%p;
}
}
return c;
}
while(n>0){
if(n&1)tt=ju(tt,m);
n=n>>1;
m=ju(m,m);
}
原题在此→http://poj.org/problem?id=3070
矩乘还有什么用→_→ ,反正我不知道了,总结一下。。矩乘可以优化转移方案是一样的DP问题……
loading...
 评论 (0)
评论 (0)